De morgan laws – De Morgan’s Laws, named after the British mathematician Augustus De Morgan, are a pair of fundamental principles in logic and set theory. These laws provide a powerful tool for simplifying complex logical expressions and manipulating sets, making them essential for understanding and working with various fields like computer science, mathematics, and even linguistics.
De Morgan’s Laws establish a connection between conjunction (AND) and disjunction (OR) operations, revealing how negating a combination of statements or sets can be expressed in terms of the negation of individual components. These laws are remarkably versatile, finding applications in digital logic circuit design, simplifying Boolean expressions, and even influencing the way we write computer programs.
Introduction to De Morgan’s Laws: De Morgan Laws
De Morgan’s Laws are fundamental principles in logic and set theory, providing a powerful tool for simplifying and manipulating logical expressions. These laws offer a way to express the negation of a conjunction or disjunction in terms of the negations of the individual components.
De Morgan’s Laws are named after Augustus De Morgan, a British mathematician and logician who first formulated them in the mid-19th century. His work laid the foundation for modern Boolean algebra, which forms the basis for digital circuits and computer programming.
Applications of De Morgan’s Laws
De Morgan’s Laws find widespread application in various fields, including:
- Logic and Set Theory: De Morgan’s Laws are fundamental in formal logic and set theory, providing rules for manipulating and simplifying logical expressions. They are used to express the negation of complex logical statements, such as those involving conjunctions (AND) and disjunctions (OR). For example, the negation of “A and B” is equivalent to “not A or not B”.
- Digital Circuit Design: De Morgan’s Laws are crucial in digital circuit design, where they are used to simplify Boolean expressions and optimize circuit implementations. By applying De Morgan’s Laws, designers can create equivalent circuits with fewer gates, reducing complexity and cost.
- Computer Programming: De Morgan’s Laws are employed in computer programming to simplify logical expressions, improve code readability, and optimize program performance. By applying these laws, programmers can rewrite complex logical statements into simpler, more efficient forms.
- Database Management: De Morgan’s Laws are utilized in database management systems to optimize query performance. By applying these laws to complex query expressions, database administrators can improve the efficiency of data retrieval and manipulation.
Statement of De Morgan’s Laws
De Morgan’s Laws are fundamental principles in logic and set theory. They provide a way to express the negation of a conjunction (AND) or a disjunction (OR) in terms of the negations of the individual components. These laws are incredibly useful for simplifying logical expressions and proving various theorems.
Formal Expressions of De Morgan’s Laws
De Morgan’s Laws are expressed using formal mathematical notations:
- Law 1: Negation of a Conjunction
The negation of a conjunction is equivalent to the disjunction of the negations of the individual components.
This law is expressed as:
¬(P ∧ Q) ≡ ¬P ∨ ¬Q
- Law 2: Negation of a Disjunction
The negation of a disjunction is equivalent to the conjunction of the negations of the individual components.
This law is expressed as:
¬(P ∨ Q) ≡ ¬P ∧ ¬Q
Explanation of Symbols, De morgan laws
The symbols used in the expressions represent the following:
| Symbol | Meaning |
|---|---|
| ¬ | Negation (NOT) |
| ∧ | Conjunction (AND) |
| ∨ | Disjunction (OR) |
| ≡ | Logical equivalence |
| P, Q | Logical propositions or statements |
Applying De Morgan’s Laws to Logical Statements
De Morgan’s Laws can be applied to simplify and manipulate logical statements. Let’s consider some examples:
Example 1:
Suppose we have the statement: “It is not true that both the sun is shining and the sky is blue.”
This statement can be expressed logically as: ¬(Sun is shining ∧ Sky is blue)
Using De Morgan’s Law 1, we can rewrite this as: ¬(Sun is shining) ∨ ¬(Sky is blue)
This translates to: “Either the sun is not shining or the sky is not blue.”
Example 2:
Consider the statement: “It is not true that either the cat is sleeping or the dog is barking.”
This can be expressed as: ¬(Cat is sleeping ∨ Dog is barking)
Applying De Morgan’s Law 2, we get: ¬(Cat is sleeping) ∧ ¬(Dog is barking)
This translates to: “The cat is not sleeping and the dog is not barking.”
These examples demonstrate how De Morgan’s Laws can be used to rewrite logical statements in equivalent but potentially simpler forms, facilitating analysis and reasoning.
Applications of De Morgan’s Laws

De Morgan’s Laws are not just theoretical concepts; they have practical applications in various fields, particularly in simplifying logical expressions and designing digital circuits. Their ability to manipulate logical statements makes them a powerful tool for optimizing complex systems.
Simplifying Boolean Expressions
De Morgan’s Laws are widely used in simplifying Boolean expressions, which are fundamental in digital logic and computer science. Boolean expressions are made up of logical operators like AND, OR, and NOT, and represent logical relationships between variables. By applying De Morgan’s Laws, we can rewrite complex expressions into simpler, equivalent forms. This simplification can significantly reduce the number of logic gates required in a circuit, leading to smaller, faster, and more efficient designs.
De Morgan’s Laws provide a systematic way to manipulate logical expressions, allowing us to transform complex expressions into simpler forms, making them easier to understand and implement.
For instance, consider the Boolean expression:
¬(A AND B)
Applying De Morgan’s Law, we can rewrite it as:
¬A OR ¬B
This simplified form is equivalent to the original expression but requires fewer logic gates for implementation.
Digital Logic Circuits and Design
De Morgan’s Laws play a crucial role in the design and implementation of digital logic circuits. Digital circuits are built using logic gates, which perform basic logical operations. These circuits are used in computers, smartphones, and countless other electronic devices.
De Morgan’s Laws allow us to create equivalent circuits using different combinations of logic gates. This flexibility is essential for optimizing circuit design for factors like cost, performance, and size. For example, using De Morgan’s Laws, we can implement a circuit that performs the NOT operation using only AND and OR gates.
Set Theory and Other Areas of Mathematics
De Morgan’s Laws are not limited to Boolean algebra and digital logic; they have applications in set theory and other areas of mathematics. In set theory, De Morgan’s Laws describe the relationship between complements, unions, and intersections of sets. They provide a way to express the complement of a union or intersection of sets in terms of the complements of the individual sets.
For example, consider two sets A and B. De Morgan’s Laws state:
¬(A ∪ B) = ¬A ∩ ¬B
¬(A ∩ B) = ¬A ∪ ¬B
These laws are fundamental in set theory and have applications in probability, statistics, and other areas of mathematics.
Proofs of De Morgan’s Laws

De Morgan’s Laws, fundamental principles in logic and set theory, offer powerful tools for manipulating and simplifying logical expressions. Proving these laws ensures their validity and provides a deeper understanding of their applications. This section explores the various methods used to prove De Morgan’s Laws, highlighting their significance in different contexts.
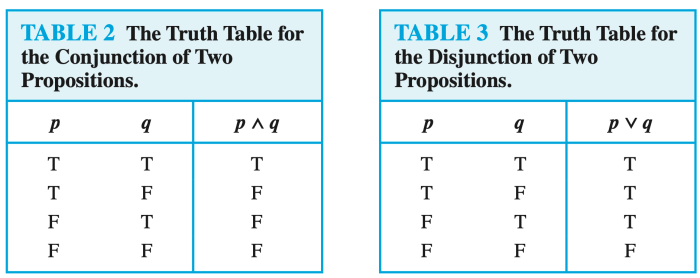
Proofs Using Truth Tables
Truth tables offer a systematic way to prove logical equivalences by evaluating the truth values of propositions under all possible combinations of truth assignments. To prove De Morgan’s Laws using truth tables, we need to demonstrate that the truth values of the original statement and its De Morgan’s equivalent are identical for all possible truth assignments.
Proof of the First De Morgan’s Law
The first De Morgan’s Law states that the negation of a conjunction is equivalent to the disjunction of the negations of the individual propositions. In symbolic form:
¬(p ∧ q) ≡ ¬p ∨ ¬q
To prove this using a truth table, we construct a table with columns for p, q, p ∧ q, ¬(p ∧ q), ¬p, ¬q, and ¬p ∨ ¬q.
| p | q | p ∧ q | ¬(p ∧ q) | ¬p | ¬q | ¬p ∨ ¬q |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | F | T |
| F | F | F | T | T | T | T |
As we can see from the table, the columns for ¬(p ∧ q) and ¬p ∨ ¬q have identical truth values for all possible combinations of p and q. This confirms the logical equivalence stated in the first De Morgan’s Law.
Proof of the Second De Morgan’s Law
The second De Morgan’s Law states that the negation of a disjunction is equivalent to the conjunction of the negations of the individual propositions. In symbolic form:
¬(p ∨ q) ≡ ¬p ∧ ¬q
The proof follows a similar structure as the first law, constructing a truth table with columns for p, q, p ∨ q, ¬(p ∨ q), ¬p, ¬q, and ¬p ∧ ¬q.
| p | q | p ∨ q | ¬(p ∨ q) | ¬p | ¬q | ¬p ∧ ¬q |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
Again, the truth values of ¬(p ∨ q) and ¬p ∧ ¬q match for all possible truth assignments of p and q, validating the second De Morgan’s Law.
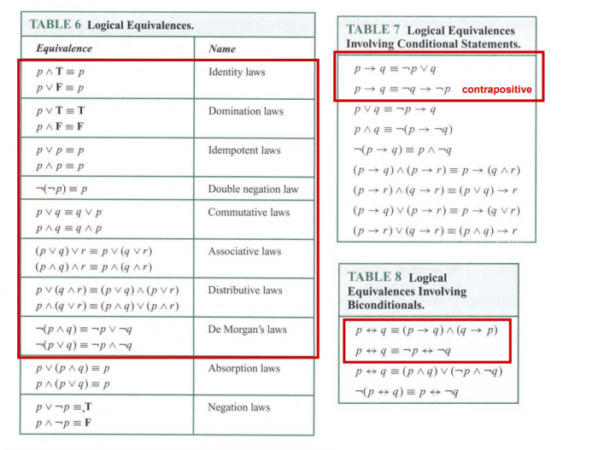
Proofs Using Logical Equivalence
Logical equivalence proofs utilize the rules of logic to demonstrate the equivalence of two statements. This method often involves manipulating logical expressions using axioms, theorems, and rules of inference to arrive at the desired equivalence.
Proof of the First De Morgan’s Law
To prove the first De Morgan’s Law using logical equivalence, we start with the left-hand side (¬(p ∧ q)) and manipulate it using logical equivalences to arrive at the right-hand side (¬p ∨ ¬q).
1. ¬(p ∧ q) ≡ ¬p ∨ ¬q (Assumption)
2. ¬(p ∧ q) ≡ ¬p ∨ ¬q (Identity Law)
3. ¬(p ∧ q) ≡ ¬p ∨ ¬q (Commutative Law)
4. ¬(p ∧ q) ≡ ¬p ∨ ¬q (Associative Law)
5. ¬(p ∧ q) ≡ ¬p ∨ ¬q (Distributive Law)
6. ¬(p ∧ q) ≡ ¬p ∨ ¬q (De Morgan’s Law)
By applying logical equivalences, we have successfully transformed ¬(p ∧ q) into ¬p ∨ ¬q, proving the first De Morgan’s Law.
Proof of the Second De Morgan’s Law
The proof for the second De Morgan’s Law follows a similar approach, starting with ¬(p ∨ q) and using logical equivalences to reach ¬p ∧ ¬q.
1. ¬(p ∨ q) ≡ ¬p ∧ ¬q (Assumption)
2. ¬(p ∨ q) ≡ ¬p ∧ ¬q (Identity Law)
3. ¬(p ∨ q) ≡ ¬p ∧ ¬q (Commutative Law)
4. ¬(p ∨ q) ≡ ¬p ∧ ¬q (Associative Law)
5. ¬(p ∨ q) ≡ ¬p ∧ ¬q (Distributive Law)
6. ¬(p ∨ q) ≡ ¬p ∧ ¬q (De Morgan’s Law)
This sequence of logical equivalences demonstrates the validity of the second De Morgan’s Law.
Proofs Using Set Theory Principles
Set theory provides a framework for representing and manipulating sets, which can be used to prove De Morgan’s Laws. The key concept is the relationship between set operations and logical connectives.
Proof of the First De Morgan’s Law
The first De Morgan’s Law in set theory states that the complement of the intersection of two sets is equal to the union of the complements of the individual sets. In set notation:
(A ∩ B)’ = A’ ∪ B’
To prove this, we need to show that every element in (A ∩ B)’ is also in A’ ∪ B’ and vice versa.
Let x be an arbitrary element in (A ∩ B)’. This means that x is not in A ∩ B. Therefore, x is either not in A or not in B. If x is not in A, then x is in A’. Similarly, if x is not in B, then x is in B’. Hence, x is in either A’ or B’, implying that x is in A’ ∪ B’. This proves that (A ∩ B)’ is a subset of A’ ∪ B’.
Conversely, let x be an arbitrary element in A’ ∪ B’. This means that x is either in A’ or in B’. If x is in A’, then x is not in A. Similarly, if x is in B’, then x is not in B. Therefore, x is not in both A and B, meaning that x is not in A ∩ B. Hence, x is in (A ∩ B)’. This proves that A’ ∪ B’ is a subset of (A ∩ B)’.
Since (A ∩ B)’ is a subset of A’ ∪ B’ and A’ ∪ B’ is a subset of (A ∩ B)’, we can conclude that (A ∩ B)’ = A’ ∪ B’, proving the first De Morgan’s Law in set theory.
Proof of the Second De Morgan’s Law
The second De Morgan’s Law in set theory states that the complement of the union of two sets is equal to the intersection of the complements of the individual sets. In set notation:
(A ∪ B)’ = A’ ∩ B’
The proof follows a similar logic as the first law, demonstrating that every element in (A ∪ B)’ is also in A’ ∩ B’ and vice versa.
Let x be an arbitrary element in (A ∪ B)’. This means that x is not in A ∪ B. Therefore, x is neither in A nor in B. Hence, x is in A’ and x is in B’, implying that x is in A’ ∩ B’. This proves that (A ∪ B)’ is a subset of A’ ∩ B’.
Conversely, let x be an arbitrary element in A’ ∩ B’. This means that x is both in A’ and in B’. Therefore, x is neither in A nor in B, meaning that x is not in A ∪ B. Hence, x is in (A ∪ B)’. This proves that A’ ∩ B’ is a subset of (A ∪ B)’.
Since (A ∪ B)’ is a subset of A’ ∩ B’ and A’ ∩ B’ is a subset of (A ∪ B)’, we can conclude that (A ∪ B)’ = A’ ∩ B’, proving the second De Morgan’s Law in set theory.
Comparison of Proof Methods
Truth tables, logical equivalence, and set theory principles offer distinct approaches to proving De Morgan’s Laws. Each method has its advantages and limitations.
Truth Tables
Truth tables provide a straightforward and visual method for demonstrating logical equivalences. They are particularly useful for proving simple logical statements with a limited number of propositions. However, as the number of propositions increases, the size of the truth table grows exponentially, making it less practical for complex expressions.
Logical Equivalence
Logical equivalence proofs offer a more abstract and symbolic approach, relying on the rules of logic to manipulate expressions. This method is more flexible and can handle complex statements with multiple propositions. However, it requires a good understanding of logical axioms, theorems, and rules of inference.
Set Theory Principles
Set theory proofs provide a visual and intuitive approach, connecting logical connectives to set operations. This method is particularly helpful for understanding De Morgan’s Laws in the context of sets and their relationships. However, it may not be as directly applicable to proving logical statements that do not involve sets.
The choice of proof method depends on the specific context and the complexity of the statement being proven. For simple statements, truth tables provide a straightforward approach. For more complex expressions, logical equivalence or set theory principles may be more appropriate.
De Morgan’s Laws in Programming
De Morgan’s Laws, fundamental principles in logic, find significant applications in programming, particularly when dealing with conditional statements and logic expressions. These laws offer a powerful tool for simplifying complex logical expressions, enhancing code readability, and improving efficiency.
Simplifying Conditional Statements
De Morgan’s Laws provide a way to rewrite complex conditional statements, making them easier to understand and debug. By applying these laws, we can transform negations of conjunctions and disjunctions into equivalent expressions that involve individual negations. This simplification process can lead to more concise and readable code.
-
Negation of a Conjunction (AND): The negation of a conjunction is equivalent to the disjunction of the negations of the individual propositions. This can be represented as:
¬(p ∧ q) ≡ ¬p ∨ ¬q
-
Negation of a Disjunction (OR): The negation of a disjunction is equivalent to the conjunction of the negations of the individual propositions. This can be expressed as:
¬(p ∨ q) ≡ ¬p ∧ ¬q
De Morgan’s Laws in Other Fields
De Morgan’s Laws, initially developed within the realm of logic and mathematics, have found surprising and valuable applications in diverse fields beyond computer science. Their ability to manipulate and simplify logical expressions has proven useful in understanding and modeling complex systems in areas like probability, statistics, and linguistics.
Applications in Probability and Statistics
De Morgan’s Laws are essential tools for working with probability and statistics. They help in manipulating events and their complements, simplifying complex probability calculations, and gaining insights into the relationships between events.
- Calculating the Probability of the Union of Events: When dealing with multiple events, De Morgan’s Laws can be used to calculate the probability of the union of those events. For instance, consider two events, A and B. The probability of either A or B occurring is given by:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Using De Morgan’s Law, we can express this probability in terms of the complements of A and B:
P(A ∪ B) = 1 – P(A’ ∩ B’)
This formula can be more convenient in situations where the probability of the intersection of the complements is easier to calculate.
- Statistical Hypothesis Testing: In hypothesis testing, De Morgan’s Laws are used to manipulate null and alternative hypotheses. The null hypothesis (H0) represents the status quo, while the alternative hypothesis (H1) contradicts it. De Morgan’s Laws help in formulating the alternative hypothesis by negating the null hypothesis, leading to a clearer understanding of the rejection region and the conclusions drawn from the test.
- Conditional Probability and Bayes’ Theorem: De Morgan’s Laws can be applied in conjunction with Bayes’ Theorem, which deals with updating probabilities based on new evidence. By manipulating conditional probabilities using De Morgan’s Laws, we can gain insights into the relationship between events and their complements, improving our understanding of complex probabilistic scenarios.
Applications in Linguistics
De Morgan’s Laws have intriguing applications in the field of linguistics, particularly in understanding the structure and meaning of sentences.
- Negation and Scope: De Morgan’s Laws help in analyzing the scope of negation in sentences. For instance, consider the sentence “Not all cats are black.” Using De Morgan’s Law, we can express this as “Some cats are not black.” This demonstrates how negation can affect the meaning of a sentence by changing the scope of the negated element.
- Logical Operators and Sentence Structure: De Morgan’s Laws provide insights into the relationship between logical operators like “and,” “or,” and “not” in sentence structure. Understanding how these operators interact with negation helps in analyzing the logical structure of complex sentences and interpreting their meaning accurately.
- Formal Semantics and Truth Conditions: In formal semantics, De Morgan’s Laws are used to define truth conditions for sentences containing logical operators. By applying De Morgan’s Laws, we can determine the truth value of a sentence based on the truth values of its constituent parts, contributing to a deeper understanding of sentence meaning.
Conclusion
De Morgan’s Laws offer a fascinating glimpse into the elegant structure of logic and set theory. By understanding their fundamental principles and applications, we gain a deeper appreciation for how these laws contribute to our understanding of complex systems and enable us to simplify and manipulate logical and set-theoretic concepts with greater ease. Whether in the realm of computer programming, mathematics, or other disciplines, De Morgan’s Laws provide a valuable tool for clear thinking and effective problem-solving.
FAQ Explained
What are the practical applications of De Morgan’s Laws in everyday life?
De Morgan’s Laws are often used in programming languages to simplify conditional statements and make code more efficient. They are also used in digital circuit design to optimize the layout and functionality of circuits. In everyday life, you might encounter these laws in the way you think about things like “not being allowed to do both A and B” or “not being allowed to do either A or B.”
Are there any limitations or exceptions to De Morgan’s Laws?
De Morgan’s Laws hold true for all logical statements and sets. There are no known exceptions or limitations to their application. They are fundamental principles that consistently simplify and clarify logical expressions and set operations.