De Morgan’s Laws, named after the brilliant mathematician Augustus De Morgan, provide a powerful tool for simplifying complex logical and set-theoretic expressions. These laws, essentially rules of logic, offer a way to express the negation of a conjunction (AND) or disjunction (OR) in terms of the negations of the individual components. This concept, while seemingly abstract, has profound implications across various fields, from mathematics and computer science to everyday problem-solving.
The beauty of De Morgan’s Laws lies in their ability to transform complex expressions into simpler, more manageable forms. Imagine having a long, convoluted statement that you need to understand or manipulate. De Morgan’s Laws offer a way to break down that statement into smaller, more easily digestible parts. This ability to simplify complexity is what makes these laws so valuable.
De Morgan’s Laws in Set Theory
De Morgan’s Laws are fundamental principles in set theory that provide a way to express the complement of a union or intersection of sets. They are named after Augustus De Morgan, a British mathematician who first formulated these laws in the 19th century. These laws are incredibly useful for simplifying complex set expressions and for understanding the relationship between union, intersection, and complements in set theory.
The Laws
De Morgan’s Laws state that the complement of the union of two sets is equal to the intersection of their complements, and the complement of the intersection of two sets is equal to the union of their complements.
(A ∪ B)’ = A’ ∩ B’
(A ∩ B)’ = A’ ∪ B’
Where:
* A and B are sets
* A’ represents the complement of set A
* B’ represents the complement of set B
* ∪ represents the union of sets
* ∩ represents the intersection of sets
Relationship Between Union and Intersection
De Morgan’s Laws reveal a fundamental relationship between the union and intersection of sets. They demonstrate that the complement of a union is equivalent to the intersection of complements, and vice versa. This relationship highlights the duality between these two set operations.
Visual Representation
Venn diagrams are a powerful tool for visualizing set operations. The following Venn diagram illustrates De Morgan’s first law, (A ∪ B)’ = A’ ∩ B’.
* Diagram:
* Draw two overlapping circles representing sets A and B.
* Shade the region representing the union of A and B (A ∪ B).
* The area outside the shaded region represents the complement of the union (A ∪ B)’.
* Shade the areas outside both circles representing the complements of A and B (A’ and B’).
* The overlap between these shaded areas represents the intersection of the complements (A’ ∩ B’).
Observation: The shaded region representing (A ∪ B)’ perfectly matches the shaded region representing A’ ∩ B’, illustrating the equivalence of the two expressions.
De Morgan’s Laws in Logic

De Morgan’s Laws, initially formulated for set theory, also find profound application in propositional logic. These laws offer a systematic approach to negating complex logical statements involving conjunction (AND) and disjunction (OR). They provide a means to simplify logical expressions and derive equivalent statements, enhancing our understanding of logical relationships.
Negation of Conjunction and Disjunction
De Morgan’s Laws in propositional logic establish the equivalence between the negation of a conjunction and the disjunction of the negations of the individual propositions. Similarly, the negation of a disjunction is equivalent to the conjunction of the negations of the individual propositions.
• ¬(p ∧ q) ≡ ¬p ∨ ¬q
• ¬(p ∨ q) ≡ ¬p ∧ ¬q
Where:
* ¬ represents negation (NOT)
* ∧ represents conjunction (AND)
* ∨ represents disjunction (OR)
* p and q are propositions
These laws highlight the relationship between negation and logical operators. The negation of a conjunction requires that at least one of the propositions within the conjunction is false. Conversely, the negation of a disjunction requires that all the propositions within the disjunction are false.
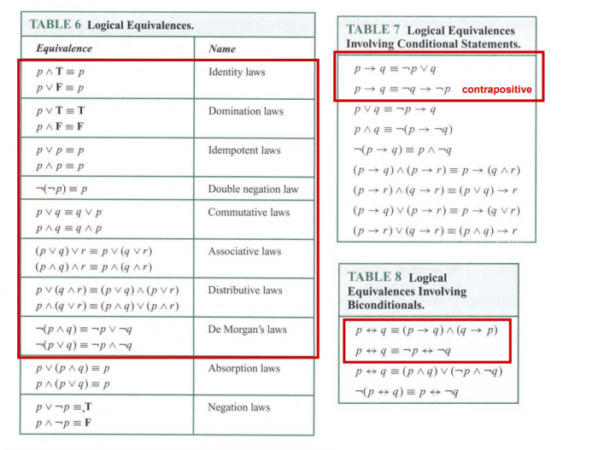
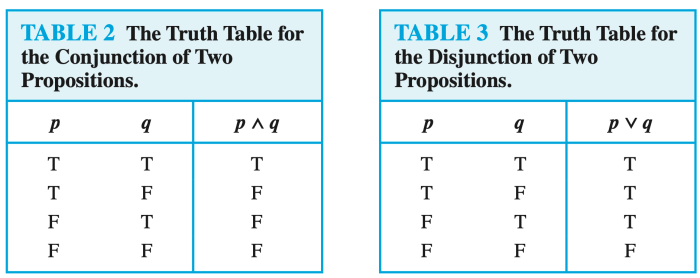
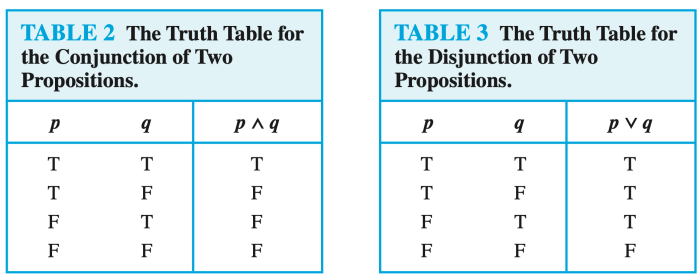
Truth Values for Logical Expressions, De morgan’s laws
The following table illustrates the truth values for different logical expressions, demonstrating the validity of De Morgan’s Laws:
| p | q | p ∧ q | ¬(p ∧ q) | ¬p | ¬q | ¬p ∨ ¬q |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | F | T |
| F | F | F | T | T | T | T |
| p | q | p ∨ q | ¬(p ∨ q) | ¬p | ¬q | ¬p ∧ ¬q |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
As evident from the tables, the truth values for ¬(p ∧ q) and ¬p ∨ ¬q are identical, validating the first De Morgan’s Law. Similarly, the truth values for ¬(p ∨ q) and ¬p ∧ ¬q are identical, confirming the second De Morgan’s Law.
Applications of De Morgan’s Laws
De Morgan’s Laws are not just abstract mathematical concepts; they have practical applications in various fields, particularly in logic, computer science, and electrical engineering. These laws allow us to simplify complex logical expressions, making them easier to understand and analyze. They also play a crucial role in designing circuits and writing efficient code.
Real-World Applications
De Morgan’s Laws are widely used in various real-world scenarios, making complex logical expressions easier to understand and manipulate. Here are a few examples:
- Computer Programming: In programming, De Morgan’s Laws are used to simplify complex logical expressions within conditional statements and loops. For instance, when checking if a variable is within a certain range, De Morgan’s Laws can be used to rewrite the condition in a more efficient way.
- Circuit Design: De Morgan’s Laws are fundamental in designing logic gates and circuits. They help simplify complex circuit designs, leading to more efficient and cost-effective solutions. For example, in a circuit with multiple AND gates, De Morgan’s Laws can be used to replace them with a single NOT gate followed by an OR gate.
- Database Queries: De Morgan’s Laws are used in database management systems to optimize complex queries. By simplifying logical expressions in queries, they improve query performance and efficiency.
Simplifying Logical Expressions
De Morgan’s Laws are instrumental in simplifying complex logical expressions, making them easier to understand and analyze. Here’s how:
- Negation of Conjunction: The first law states that the negation of a conjunction (AND) is equivalent to the disjunction (OR) of the negations of the individual propositions. This can be represented as:
¬(p ∧ q) ≡ ¬p ∨ ¬q
- Negation of Disjunction: The second law states that the negation of a disjunction (OR) is equivalent to the conjunction (AND) of the negations of the individual propositions. This can be represented as:
¬(p ∨ q) ≡ ¬p ∧ ¬q
Hypothetical Problem
Consider a scenario where a company wants to grant access to a secure system based on two conditions:
- Condition 1: The user must be an employee of the company.
- Condition 2: The user must have a valid security clearance.
Access is granted only if both conditions are met. This can be represented as:
Access = Employee AND Clearance
Now, suppose the company wants to restrict access to those who do not meet both conditions. Using De Morgan’s Law, we can rewrite the expression as:
¬(Access) = ¬(Employee AND Clearance) ≡ ¬Employee OR ¬Clearance
This simplified expression means that access is denied if the user is not an employee OR does not have a valid security clearance.
De Morgan’s Laws in Digital Circuits

De Morgan’s Laws, originally formulated in the realm of set theory and logic, find a powerful application in the design and optimization of digital circuits. They provide a fundamental principle for simplifying complex logic expressions and manipulating circuit structures, leading to more efficient and cost-effective implementations.
Relationship Between Logic Gates and De Morgan’s Laws
De Morgan’s Laws directly relate to the fundamental building blocks of digital circuits: logic gates. Logic gates perform Boolean operations on binary inputs (0 or 1), producing a binary output. The core of De Morgan’s Laws lies in their ability to express the negation of a logical operation (AND or OR) in terms of the negation of individual inputs.
- NOT Gate: The NOT gate inverts the input. If the input is 0, the output is 1, and vice versa. This is represented by the symbol ¬ or an overline (e.g., ¬A or A̅).
- AND Gate: The AND gate outputs a 1 only if all its inputs are 1. Otherwise, it outputs a 0. This is represented by the symbol ∧ or a dot (e.g., A ∧ B or A ⋅ B).
- OR Gate: The OR gate outputs a 1 if at least one of its inputs is 1. It outputs a 0 only if all inputs are 0. This is represented by the symbol ∨ or a plus sign (e.g., A ∨ B or A + B).
De Morgan’s Laws provide an elegant way to express the negation of AND and OR operations:
De Morgan’s Law 1: ¬(A ∧ B) = ¬A ∨ ¬B
De Morgan’s Law 2: ¬(A ∨ B) = ¬A ∧ ¬B
These laws demonstrate that the negation of an AND operation is equivalent to the OR operation of the negated inputs, and vice versa.
Applications in Digital Circuit Optimization
De Morgan’s Laws are instrumental in simplifying logic expressions and optimizing digital circuits. By applying these laws, we can:
- Reduce the number of gates: Complex logic expressions can often be simplified using De Morgan’s Laws, reducing the number of gates required in the circuit. This leads to smaller, more compact designs and lower power consumption.
- Convert between different gate types: De Morgan’s Laws allow us to convert AND gates to OR gates and vice versa, providing flexibility in circuit design and implementation.
- Simplify Boolean expressions: By applying De Morgan’s Laws, we can manipulate Boolean expressions to arrive at simpler, equivalent forms, which can be easier to understand and implement.
For instance, consider a circuit that implements the expression ¬(A ∧ B ∧ C). Using De Morgan’s Law 1, we can rewrite this as ¬A ∨ ¬B ∨ ¬C. This simplification eliminates the need for a three-input AND gate, replacing it with three NOT gates and a three-input OR gate. This can lead to a more efficient and cost-effective circuit design.
Conclusive Thoughts
From simplifying complex logic expressions in computer programming to understanding the relationships between sets in mathematics, De Morgan’s Laws provide a valuable tool for anyone working with logical concepts. Their ability to transform complex statements into simpler forms makes them indispensable in various fields, highlighting their enduring importance in the world of logic and beyond.
Query Resolution
What are the two main De Morgan’s Laws?
The two main De Morgan’s Laws are:
* Not (A and B) is equivalent to (Not A) or (Not B)
* Not (A or B) is equivalent to (Not A) and (Not B)
How do De Morgan’s Laws apply to real-world situations?
Imagine a situation where you need to find someone who is not a doctor and not a lawyer. Using De Morgan’s Laws, you can rephrase this as “someone who is not (a doctor or a lawyer).” This simplifies the search process.
What are some practical applications of De Morgan’s Laws in digital circuits?
De Morgan’s Laws are used to simplify logic gates in digital circuits, which can lead to more efficient and cost-effective designs. For example, you can use De Morgan’s Laws to create a circuit that performs the AND operation using only OR gates and inverters.